The last post was about classifying areas inside caves as rooms, where the joins between the rooms were, and where we might spawn game features such as loot, boss fights, or NPC dwellings and the like. All our examples were based on an abstract shape, though, which was rather smooth. Notably, unlike any surfaces in Sun Shy. However, this is not a problem limited to Sun Shy – any game world with a grid of any kind, including oldschool 2D games with bitmap-based destructible terrain (like Worms), can potentially suffer from this problem.

A quick recap. Have a look at this image:

This is roughly what a ‘flat’ piece of ground looks like in Sun Shy. Because of the irregular grid, this is as flat as it gets. This is an area that we might hope to identify as flat ground, that a player might walk across. They certainly can walk across it – the control system described here allows it – but let’s look at the naïvely calculated normals:

These normals are all over the place – occasionally one points straight up, but lots of them are pointing in weird directions. We need a way of smoothing them out, to get the broad sense of the direction of the surface.

In the case of Sun Shy, it makes sense to look at the ‘normals’ for the tiles, rather than the boundaries between the tiles (for most purposes, the tiles are the things that have information attached to them, so this is useful for navigation markup and the like). If it sounds like nonsense to have a normal associated with a tile centre, that’s because mathematically it is – but, let’s go with it for now.

Here’s a zoomed in section of the above Voronoi tessellation.

We’re going to calculate the ‘normal’ for the tile right there in the middle. We’re going to do it by looking at the centre point of every neighbouring tile that has dirt in it, here noted in red:

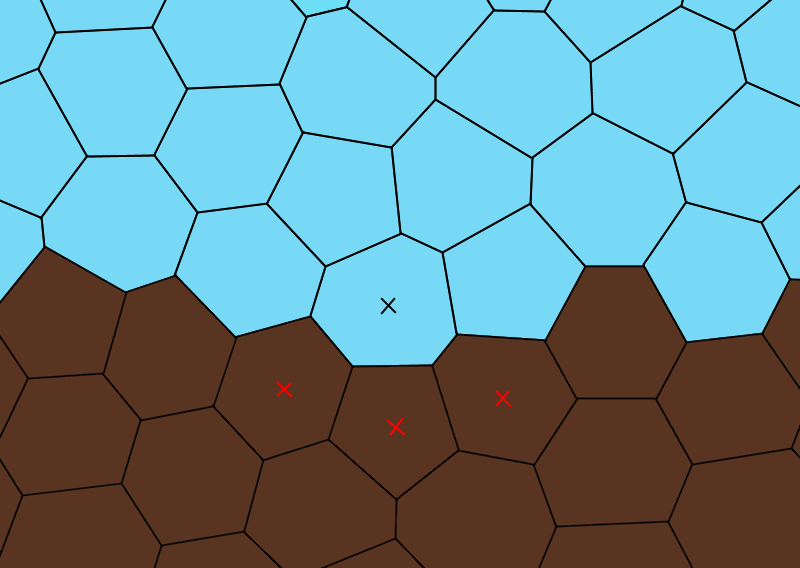
We then calculate the average position of those neighbours, and draw a line from that average position, through the centre of our main tile. That’s our tile normal!

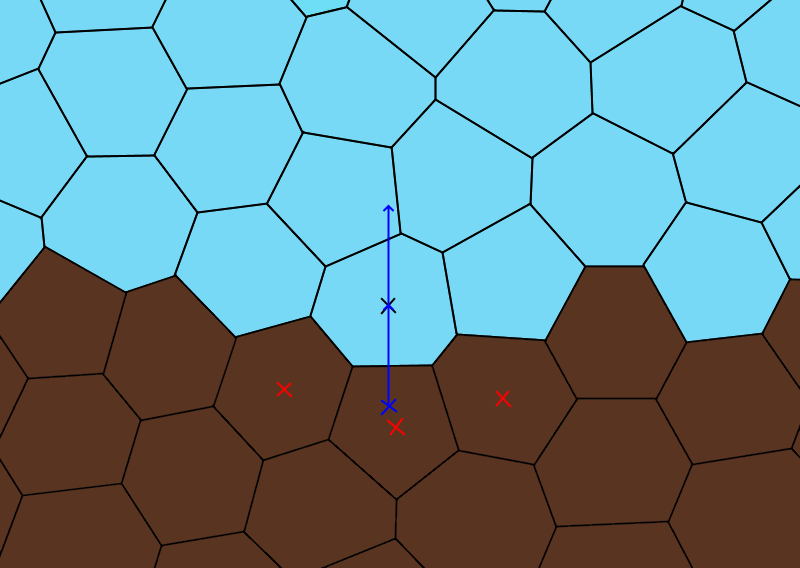
As we can see here, this is a pretty good result – if we apply the same approach to all the empty tiles here that are next to filled tiles, we see things are looking pretty good:

Looking pretty good, but not perfect. After all, this is as flat a surface as the tile grid can possibly provide – we should be able to recognise it as such, in spite of some inevitable lumps. To solve this, I’ve simply averaged the normals of every tile with its direct neighbours. Instead of drawing another version of the above diagram, I’ll show this in action in Sun Shy.

Although we’re never going to get the normals uniformly pointing straight up, here, I think they’re looking pretty good – those red lines pointing upwards come close enough to representing what I would intuitively call the direction of the walls/floor/ceiling.

From here, it should be pretty straightforward to grab adjacent tiles with a sufficiently upward-pointing normal to define a floor area, which gets us the rest of the way we need to classifying the rooms from the previous post as walkable or not.

What about games that aren’t Sun Shy?

Indeed, the big point of this work has been to find techniques that can be applied outside of Sun Shy, and this post has mostly been specific to Sun Shy’s irregular grid set up, which pretty much nobody every uses. This technique actually has some value in unexpected places, though.

If you’re making a square grid game, you’re not going to have any trouble identifying floors or ceilings or walls – those directions can be represented on a square grid perfectly. However, sometimes you want to recognise other patterns, especially if your tiles are very small – for instance, the size of a single pixel. Let’s say you’re making a worms-style game – tiles get dug out by explosions, and when that happens you simply have a big 2D array of booleans that has a circular chunk cut out of it, like this:

Naturally, detecting collisions with this is no problem – you take a position, look up to see if that ‘pixel’ is black, if it is, that’s a collision. Easy! But what if you want one of your weapons to be, say, a laser cannon that reflects off what it hits. (A better example is probably a grenade that bounces around, but I don’t have the parabola drawing skills for that.) So you want it to do something like this:

How do we do that? Clearly, we need a surface normal, but the actual ‘geometry’ only has vertical and horizontal edges. That’s where (a modified version of) the above algorithm can save us. What we need is to take a box of pixels around the pixel we’ve collided with. Within that box, we’re going to obtain the average location of all the black pixels, and the average location of all the white pixels. Then, we simply draw a vector from the average black pixel position to the average white pixel position, normalise it, and that’s our surface normal.

It should be noted that if you’re looking for anything mathematically correct, you probably shouldn’t be using a grid of bools for your collision system. But if you just want things to look reasonably decent, this system works quite well. The bigger the box you use to average the pixels, the more broad patterns this will pick up on, and the more finer detail will get lost. It’s also possible to precompute the normals of a shape like this, and only update areas that get affected – this could speed things up a lot if you’re doing a large number of collision checks every frame (for instance, if you have lots of particles that are bouncing around in the environment).

Note that you do need to check for a broken case here – if you have, for instance, a collision grid that is organised like a checkerboard for some reason, and your box is an odd number of pixels wide/high, this technique will cause a divide by zero error when you try to normalise the vector at the end. There are other situations where this could conceivably happen, but only cases where there’s no good value for the normal anyway. Even so, if it somehow comes up, better to have some weird normal calculated than throwing an exception or crashing.

Next time…

The last big piece of research I carried out was about getting a character to animate convincingly on irregular surfaces. This one got complicated. I’ll be writing a bunch more about that soon.